OK — here's my deep thought for the day. Or it may not be deep, but I haven't finished my first coffee yet…
Is Hume's Maxim simply a restatement of Bayesian Inference?
I'm sure this is not a new idea, but I hadn't made the connection before. Hume's Maxim, which I've always liked, basically states that:
no testimony is sufficient to establish the existence of a miracle, unless it is more likely that the miracle occurred than that the testimony was false.
(I paraphrase slightly. More info here.)
Bayes' Rule is a little more complex, so hang while I just make some more coffee… Ok. Brace yourself. This won't hurt much.
It's the following equation:
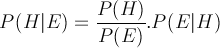
where P ( X | Y ) means 'the probability of X given Y'. It’s often written using H and E for hypothesis and evidence.
It says that you can calculate the probability of a hypothesis (say, that a miracle occurred) given some piece of evidence (Mrs Jones reports having seen it).
The probability will depend on three things in the right-hand side of the equation:
- P(H) – The probability of the miracle itself independent of any reports. (e.g. did the laws of physics change on this particular day for Mrs Jones?)
- P(E) – The probability that the evidence would present itself independent of anything actually occurring. The combination of possibilities that Mrs Jones was either mistaken, deceived, deluded, fibbing or had some other motivation — possibly a perfectly good one — for coming up with such a report in any case.
- P(E|H) – The likelihood that Mrs Jones would have reported a miracle, given that it actually occurred. Well, we’re not interested in miracles that happen quietly in the middle of a wood somewhere. We’re talking here about miracles for which there is testimony, so this term is probably 1 or close to it* and so can be removed from the equation in this case. David Hume didn’t include it. It’s worth noting, though, that if people are often abducted by aliens and neglect to mention it, you need to take that into account when they do.
If the likelihood of the laws of physics changing are greater than that Mrs Jones’s report is mistaken – i.e. that P ( H ) is greater than P ( E ) – then the probability that the miracle occurred, given her testimony, is greater than one – i.e. her testimony has established the veracity of the miracle.
So the statements are saying very similar things. Interestingly, they date from about the same period, too – late 18th century – and show an unusual overlap of two magesteria – philosphy and mathematics.
For such a simple equation, Bayes' Rule is incredibly powerful, though its revelations can sometimes be hard to grasp intuitively. You benefit from it every day, though, because it turns out to be phenomenally good, for example, at working out the likelihood that a given piece of email is spam. And a deep understanding of it, combined with a good marketing team, was the foundation of Autonomy, the Cambridge company sold to Hewlett-Packard last year for $10bn.
Sadly, it isn't used often enough for assessing the reliability of conspiracy theories and Daily Mail articles, perhaps because it doesn't tend to stick in one's mind.
So for normal, day-to-day understanding of the world around you, I recommend David Hume's version.
* Update: The probability that I will get statistics correct without help is about the same as the probability that Status-Q’s author is more intelligent than its readers. Thomas points out, quite rightly, that a probability can’t be greater than 1 – something that had been bothering me a bit too! P(E|H) is always less than P(E), so all this is really saying is that the likelihood of a miracle having occurred given Mrs Jones’s report is a bit less than the likelihood of a miracle having occurred. I may be pushing a few things too far: not least my understanding of stats. Hume is talking about the relative values of P(x), not the relationship between them. Can we draw anything more from this? A topic for discussion…!
Recent Comments