Tag Archives: statistics

Keeping things in proportion

Yesterday, in response to another thread about the AstraZeneca vaccine concerns, I tweeted,

“I hear there’s also a risk of having a car accident while driving to or from your AZ vaccination! Why is this not being revealed to the public?”

Which got some cheery replies, like,

“You could be run over walking from your car too, these car parks are dangerous places!”

And Clive Brown responded with a quick back-of-the-envelope calculation which showed that, yes, indeed, if you drove 6 miles for your vaccine, an accident was more likely than a blood clot.

Getting mine tomorrow, if I survive the journey…

Possibly-related posts:

The commercialisation of grade inflation

Google is running a particularly fatuous advertisement at the moment, clearly designed to appeal to the heart rather than the head. It appears at the start of almost every YouTube video I watch, so I see it several times per day.

“Local businesses have been there for us this year”, says the actor. “It’s time we return the love. Just leave a Google review! Because Google reviews help local businesses stay strong!”

Isn’t that nice? We may be a big cloud-based multinational but we care about the businesses on your local high street.

Now, almost everything about this is wrong. There’s the basic factual inaccuracy: local businesses often haven’t been there for us, poor things — it’s the online businesses that have kept people supplied while they’re shielding. Au contraire, we’ve often ‘been there’ for the local businesses: I’ve often been going out of my way to try and buy from local shops when it would be cheaper, easier and, of course, much safer to buy online. But that phrase is just an appeal to the emotions, so let’s not take it too literally!

No, what bugs me in the ad is the assumption, of course, that they’re good local businesses and you’re leaving them a 5-star review. Which, let’s face it, almost everybody does these days, and I’m no exception, because who wants to be the bad guy who docks them stars for what might seem like trivial complaints? And so we end up in the ridiculous situation of comparing shops, hotels, cafes etc based on whether they have a 4.6-star average or a 4.8-star one.

In a perfect world, the average business or product would have an average of three stars out of five. And we’d have a nice gaussian distribution around that: things slightly better than average would edge up towards four stars while those that were a bit unimpressive would be down in the twos. Only those that were so exceptional that they couldn’t really be improved in any way would get close to five.

It is, of course, part of life, and the same thing has always happened with A-level results, University degrees and so forth. (I have some nice stories from University colleagues about this, but they had better wait for another time.)

So I’d like to see Google run a new set of ads after this one. “Weed out dodgy businesses by leaving a low Google review! Because low reviews help customers like you stay safe.”

Somehow, I can’t see that happening.

There is another way to make reviews actually useful again, of course: Google, Amazon etc could simply revalue the currency: modify all the reviews so that the mean value was three and the standard deviation was appropriate to have a sensible number of twos and fours. You’d need to do it in a fairly sophisticated way, but it’s not rocket science. And you’d need to make sure everybody knew you were doing it, so that there was no misunderstanding.

I suggest a big advertising campaign: “Google Reviews: now the most useful on the planet!” They could put it at the beginning of all the YouTube videos. And it would get five stars from me.

Possibly-related posts:

And then three come along at once…

If you go to a bus stop where the bus arrives, on average, every 10 minutes, how long will you wait?

5 minutes, on average, right?

Wrong.

This is an example of The Inspection Paradox, a phenomenon of which I was dimly aware, but I came across some nice examples in my reading this morning – and it’s an important thing to understand.

You see, 5 minutes would be the right answer if the bus came at exactly evenly-spaced 10 minute intervals. But this doesn’t happen, at least, not outside Switzerland. So the gaps may be bigger or smaller.

If you arrive at a random time, you are more likely to hit one of the bigger gaps. The average waiting time that you, as a passenger, will experience, will therefore be higher. (Python programmers interested in a detailed analysis of this example could take a look at this blog post. If the arrival time follows a reasonably long-tailed Poisson distribution — admittedly unlikely in this particular example — then your average wait could actually be as high as 10 minutes.)

Allen Downey’s blog has a range of other nice examples in here. You can read the whole thing if you want the details, but here are a few excerpts of the key points:

A common example is the apparent paradox of class sizes. Suppose you ask college students how big their classes are and average the responses. The result might be 56. But if you ask the school for the average class size, they might say 31. It sounds like someone is lying, but they could both be right.

Basically, if you sample students at random, you are often more likely to hit students in larger classes, and that will skew your statistics if you are trying to determine the actual average class size.

That’s not necessarily a mistake. If you want to quantify student experience, the average across students might be a more meaningful statistic than the average across classes. But you have to be clear about what you are measuring and how you report it.

Here’s another travel-related example:

The same effect applies to passenger planes. Airlines complain that they are losing money because so many flights are nearly empty. At the same time passengers complain that flying is miserable because planes are too full. They could both be right. When a flight is nearly empty, only a few passengers enjoy the extra space. But when a flight is full, many passengers feel the crunch.

The Inspection Paradox is relevant to social networks, too – real or virtual.

In 1991, Scott Feld presented the “friendship paradox”: the observation that most people have fewer friends than their friends have.

If you think that everyone you know has a wider social circle than you do, it’s because you are simply more likely to be in the social circles of people with bigger social circles.

That may or may not make you feel better, but at least you now have a name for it!

Photo: Frank Hank

Update, a few days later:

As I sit in a long phone queue waiting to talk to BT, my broadband provider, I ponder just how often, on such calls, I hear the phrase, “We are experiencing a large number of calls at the moment, and we apologise for the delay…” I have often thought, that, since they always seem to be experiencing an unusually large number of calls, perhaps they need to employ some more people.

But then I realise, of course, that I am one of those large numbers. It is natural that people will experience this more often than not, because more people will be calling during the periods when more people are calling…

Possibly-related posts:

  • Happy talk? RyanAir has just announced that passengers will soon be able...
  • Big bus I reserved an economy/compact car from Avis, but when I...
  • It’s just an illusion Found this in the past, somewhere out there on the...
  • Pronto? The bus services that connect the little hill towns around...

If it doesn’t look like your normal food, that’s because it’s bait.

One of the tragedies of the accelerated ‘internet time’ is the speed at which advertisers can discover our weaknesses. It took several centuries for tabloid newspapers to evolve their attention-grabbing headlines with minimal content and maximum emotion. FURY AT VICAR’S CELEB SEX ROMPS. (‘Fury’ is a word which seems only to be used now on the front pages of tabloids and local papers.)

Of course, gentle reader, you and I would never buy a paper with that headline. Despite the temptation, we know in the end it will be unsatisfying. It’s journalistic pornography, appealing to our baser instincts. Resisting the lure is part of our education, our self-control. We laugh as we pass by, at the poor, less-intelligent souls who succomb to this ultimately unrewarding titillation.

But, in just a couple of decades, the web has allowed this process to be refined to an extreme degree. Techniques such as A/B testing enable publishers to play with content, delivering version A to one group of 10,000 viewers and version B to another 10,000 to see which delivers the most traffic/sales/ad-clicks. This can be repeated, like an iterative fractional distillation, allowing the drug to be purified as never before.

The web’s equivalent of the tabloid headline is the link text – the thing that stops you walking past and persuades you to look inside. The process can be applied there too, and we see the results everywhere: links which convey even less information and appeal purely on the gut level. “Three old grannies got up on stage and you’ll never believe what they did next!” “10 things no mother should ever do!” “This one weird tip will transform your sex life!” “The most shocking video you’ll ever see!” They are designed, of course, not to convey information, because if you had any at that point, you could decide whether or not to click. Instead, they just tell you that you really must click, because otherwise you’ll be missing out, and we’ll tell you why once you’ve done so. Because, of course, we get paid by our advertisers if you visit our site, but not if you just read the link.

Now, the tragedy is that, unlike with tabloid newspapers, the content sometimes is worth seeing. The video is amusing, or cute, or whatever, and often was carefully created to be so, because they want you to share a link on Facebook, where, of course, it will be automatically augmented with their carefully-baited title.

A group called Quick Sprout recently published a guide on How to write the perfect headline. I’m not linking to their site directly because the pop-up ads are much too annoying, but you can find it via the site above. Their tips summarise the industry’s discoveries:

  • “A writer should spend half of the entire time it takes to write a piece of persuasive content on the headline…. 8 out of 10 people will read the headline, 2 out of 10 will read the rest.”
  • “The perfect length for a headline is six words.”
  • “Use negative wording: negatives tap into our insecurities.”
  • “Try using this formula: Number or trigger word + adjective + keyword + promise.”

They have some nice examples of this last rule:

  • Before formula: “How to bathe an elephant”
  • After formula: “18 Unbelievable Ways You Can Bathe An Elephant Indoors”

But I’ve noticed a strange thing recently. I’m starting to feel ashamed when I click on links like this, as if I couldn’t resist buying the tabloid; I couldn’t help eating the junk food. I’m actively resisting sites that are linked to in this way, and I have a lower opinion of sites that display the links. Am I alone?

Take the Independent, for example, a once-reasonably-respected UK paper. The bottom of every page now looks like this:

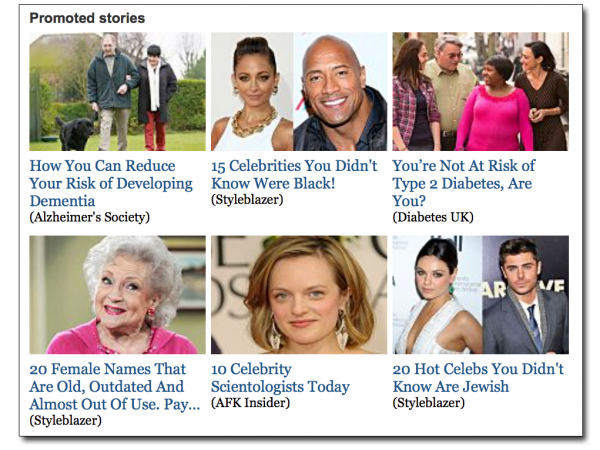
independent_ads

This is a tame set of examples which just happened to be on the first page I looked at, but really! “20 Hot Celebs You Didn’t Know Are Jewish”? We care whether they’re Jewish? They can’t be Jewish because they’re ‘hot’? Come on, Indie…! What are we meant to think of your standards?

So I hope we’ll start to see a backlash against this blatant manipulation. Let’s start educating people that, if someone pops out at you in the street and says, “Come down this alley with me, you’ll never believe what’s at the end of it!’, they may not just be doing it for your benefit.

As the old adage goes, if you can’t tell what they’re selling, it’s because you’re the product. So ask yourself this, the next time you see an irrestible link: Do you feel compelled to click, or are you making the decision?

Because there’s one sure-fire way to know if you’re the product. It’s when you’re the thing being delivered.

Possibly-related posts:

Alas, poor PC… I knew him, Bill…

An IDC press release, out today, reports that PC sales have fallen again. That’s expected now, but they’ve fallen noticeably faster than predicted: the last quarter was a surprising 14% down on the same time last year.

“At this point, unfortunately”, says an IDC staff member, “it seems clear that the Windows 8 launch not only failed to provide a positive boost to the PC market, but appears to have slowed the market…” And it’s not just Windows – Apple’s desktop/laptop sales are down, too.

A big contributor, I’m sure, is that we’ve finally reached the point where operating system manufacturers and other software developers can no longer convince users that it’s worth buying a new machine just to run their latest offerings. I’m currently a software developer, for heaven’s sake, and even I am feeling no particular desire to replace my four-year-old iMac in the near future.

But a lot of it also comes from the fact that fewer people need to do, on a regular basis, what PCs were designed to be good at doing.

Phones and tablets don’t replace a PC, but if you drew a Venn diagram of

  • What PCs do
  • What mobile devices do
  • What people do

over the last few years, it would resemble a lapsed-time animation of plate tectonics. And my point is that ‘What PCs do’ would be largely stationary, while the others moved around it in ever-more-overlapping zones…

I write quite a lot, but I use a word-processor about once a month. I manage my company accounts, but much more of that is done on a web service than on a spreadsheet. I give talks, but the days when PowerPoint was the only game in town are long gone. And I read emails… while I’m walking the dog.

So, if I’m at all typical, where does that leave Microsoft Office, the core of most PCs’ raison d’être? And remember, I’m an old guy. For most people under the age of 25, it probably never was that important. The office suite is dead, and has been for a long time. Long live the browser. On whatever device.

On which note, I should shut down the browser on this iPad and go to sleep…

Thanks to Charles Arthur for the IDC link

Possibly-related posts:

Pub Facts no. 2

And your second interesting technology statistic of the day:

  • iPhones are being born at a faster rate than people.

 

Possibly-related posts:

Pub Facts no. 1

I learned a couple of interesting technology statistics in the pub last night, and I feel it my duty to pass them on, so that you too can astound your friends at your weekend dinner parties. I'll post them separately, as a cheap ploy to increase impact and heighten suspense.

OK. Here's the first:

  • The rate at which ARM processors are being produced is approximately middle C. (around 260/sec).

Hum it to yourself for best effect.

Thanks to John Biggs of ARM for that one.

 

Possibly-related posts:

Bayeswatch

OK — here's my deep thought for the day. Or it may not be deep, but I haven't finished my first coffee yet…

Is Hume's Maxim simply a restatement of Bayesian Inference?

I'm sure this is not a new idea, but I hadn't made the connection before. Hume's Maxim, which I've always liked, basically states that:

no testimony is sufficient to establish the existence of a miracle, unless it is more likely that the miracle occurred than that the testimony was false.

(I paraphrase slightly. More info here.)

Bayes' Rule is a little more complex, so hang while I just make some more coffee… Ok. Brace yourself. This won't hurt much.

It's the following equation:

where P ( X | Y ) means 'the probability of X given Y'. It’s often written using H and E for hypothesis and evidence.

It says that you can calculate the probability of a hypothesis (say, that a miracle occurred) given some piece of evidence (Mrs Jones reports having seen it).

The probability will depend on three things in the right-hand side of the equation:

  • P(H) – The probability of the miracle itself independent of any reports. (e.g. did the laws of physics change on this particular day for Mrs Jones?)
  • P(E) – The probability that the evidence would present itself independent of anything actually occurring. The combination of possibilities that Mrs Jones was either mistaken, deceived, deluded, fibbing or had some other motivation — possibly a perfectly good one — for coming up with such a report in any case.
  • P(E|H) – The likelihood that Mrs Jones would have reported a miracle, given that it actually occurred. Well, we’re not interested in miracles that happen quietly in the middle of a wood somewhere. We’re talking here about miracles for which there is testimony, so this term is probably 1 or close to it* and so can be removed from the equation in this case. David Hume didn’t include it. It’s worth noting, though, that if people are often abducted by aliens and neglect to mention it, you need to take that into account when they do.

If the likelihood of the laws of physics changing are greater than that Mrs Jones’s report is mistaken – i.e. that P ( H ) is greater than P ( E ) – then the probability that the miracle occurred, given her testimony, is greater than one – i.e. her testimony has established the veracity of the miracle.

So the statements are saying very similar things. Interestingly, they date from about the same period, too – late 18th century – and show an unusual overlap of two magesteria – philosphy and mathematics.

For such a simple equation, Bayes' Rule is incredibly powerful, though its revelations can sometimes be hard to grasp intuitively. You benefit from it every day, though, because it turns out to be phenomenally good, for example, at working out the likelihood that a given piece of email is spam. And a deep understanding of it, combined with a good marketing team, was the foundation of Autonomy, the Cambridge company sold to Hewlett-Packard last year for $10bn.

Sadly, it isn't used often enough for assessing the reliability of conspiracy theories and Daily Mail articles, perhaps because it doesn't tend to stick in one's mind.

So for normal, day-to-day understanding of the world around you, I recommend David Hume's version.

* Update: The probability that I will get statistics correct without help is about the same as the probability that Status-Q’s author is more intelligent than its readers. Thomas points out, quite rightly, that a probability can’t be greater than 1 – something that had been bothering me a bit too! P(E|H) is always less than P(E), so all this is really saying is that the likelihood of a miracle having occurred given Mrs Jones’s report is a bit less than the likelihood of a miracle having occurred. I may be pushing a few things too far: not least my understanding of stats. Hume is talking about the relative values of P(x), not the relationship between them. Can we draw anything more from this? A topic for discussion…!

Possibly-related posts:

Fear of flying

Here’s an interesting article published in Psychological Science in 2004.

Basically, the results suggested that in the first few months following 9/11, because many more people in the States drove their cars longer distances, being fearful of flying, the increased number of deaths on the roads were actually greater than the number of people who died in the 9/11 planes.

There are some who disagree with their conclusion, saying that we don’t really know the reasons why people chose to drive instead of flying. Rose suggested that people may have opted for the car because they feared, not the flying, but the long security procedures at the airports!

But an interesting study, none the less, I thought.

Possibly-related posts:

Facing the Facebook facts

In the early days of Facebook, I found it rather annoying – there were just too many invitations from people which would have involved installing applications in my account. So I focused on the more streamlined Twitter, and many of my friends seem to have done the same.

But I’m definitely in the minority. Facebook publishes detailed statistics about their users, presumably because they are rightly proud of the numbers. 350M active users, of whom, on any given day, 50% log in, and 10% update their status at least once.

Twitter doesn’t publish any stats, but even the most optimistic estimates suggest they have less than a tenth of these numbers. For all the recent attention, it does seem as if they have a long way to go to be anything like as influential as Facebook, and such graphs as I’ve been able to find suggest that usage has declined over the last six months.

Anyone know of any reliable stats?

.

Possibly-related posts:

Feeds

RSS  RSS feed

Categories

December 2024
M T W T F S S
 1
2345678
9101112131415
16171819202122
23242526272829
3031  

© Copyright Quentin Stafford-Fraser