“I expect our sales”, says the marketing manager confidently, “to have an inflection point in Q1 next year”.
This is a pet peeve of mine. I’ve often heard sales and marketing types, and even economists and scientists who should know better, use ‘inflection point’ simply to mean ‘a sudden change in the direction I’d prefer’. Perhaps they think an inflection point is the sharp bend in a hockey-stick-type curve, or the lowest point on a line that is about to turn upwards.
In fact, an inflection (or occasionally ‘inflexion’) point on a graph is technically where the second derivative is zero and changes sign: i.e. where the gradient changes from decreasing (or increasing) to increasing (or decreasing). Another way to think of it is that, viewed from the side, the line changes from concave to convex, or vice versa.
So, typically, an inflection point looks like this:
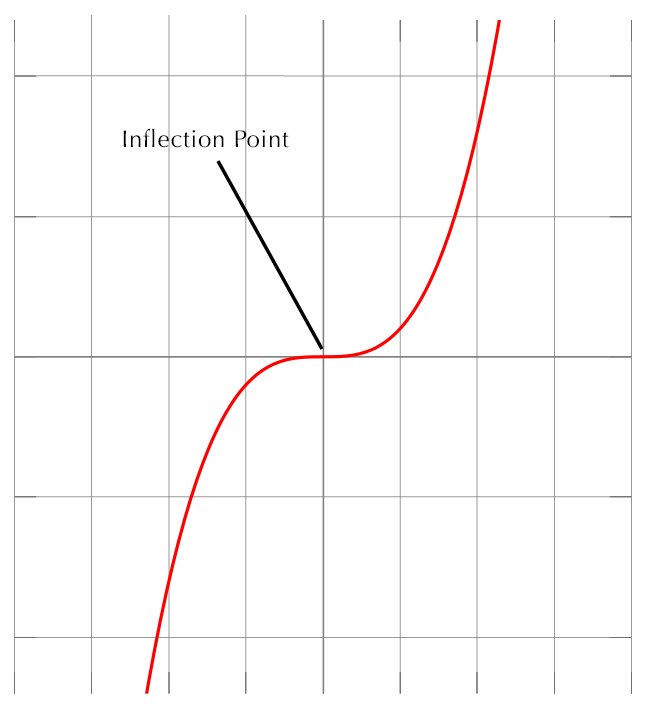
But, when touting your sales figures, remember that this is also an inflection point:
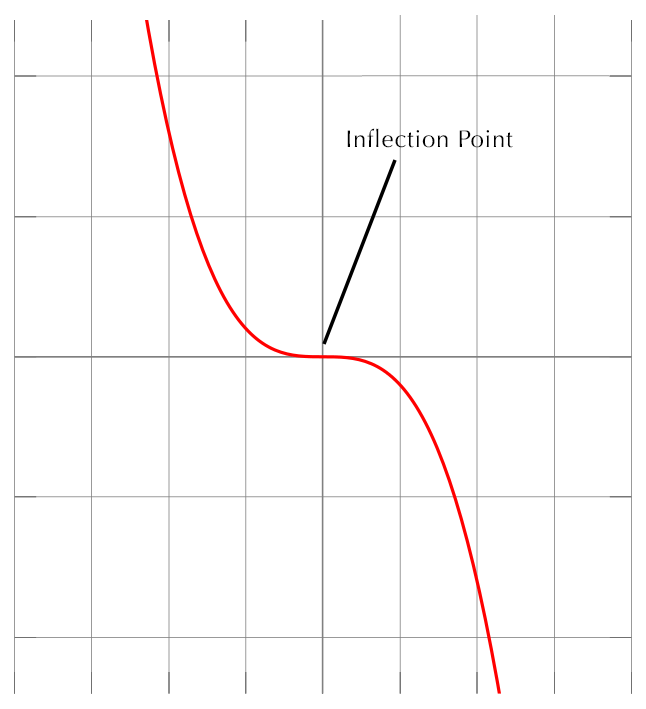
And so is this:
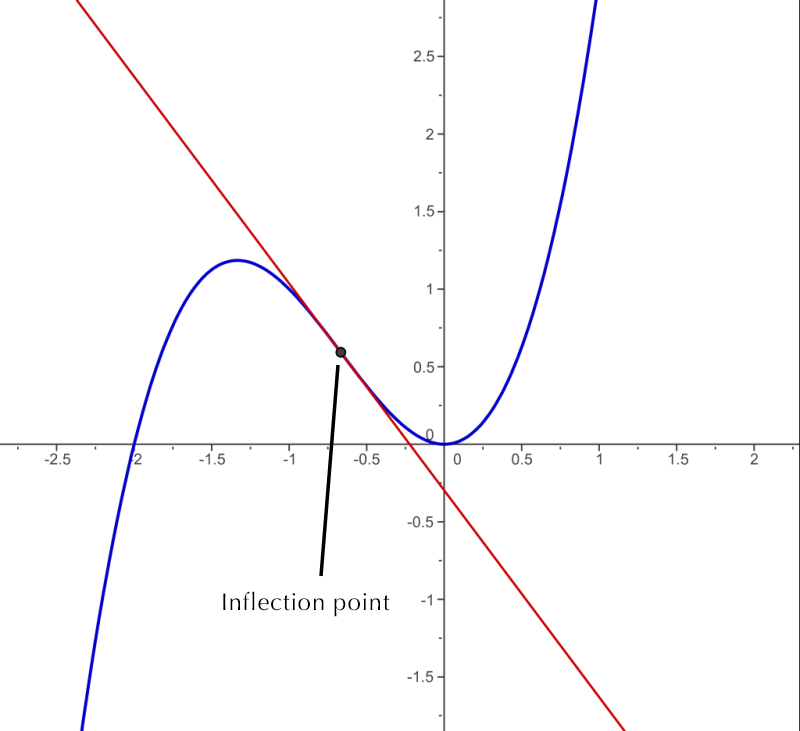
Doing a quick search, I came across an article from Thoughtworks all about inflection points and how they are important to your business. Sadly, they get it completely wrong.
As a technology leader, a portion of your analysis should revolve around determining inflection points, the critical phases of transitions along a technology’s journey from an abstract idea to maturity.
Inflection points are the points at which a product becomes a trend (something that will be used by a critical mass and therefore likely to drive value) instead of a fad (something that will fizzle out).
And here’s their illustration:
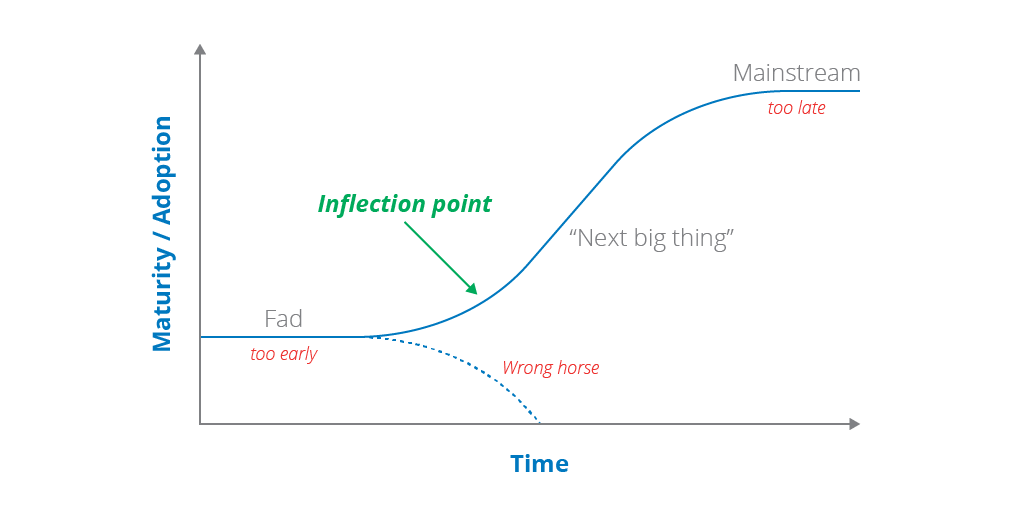
But you, gentle reader, know better. That’s not an inflection point! This is an inflection point:
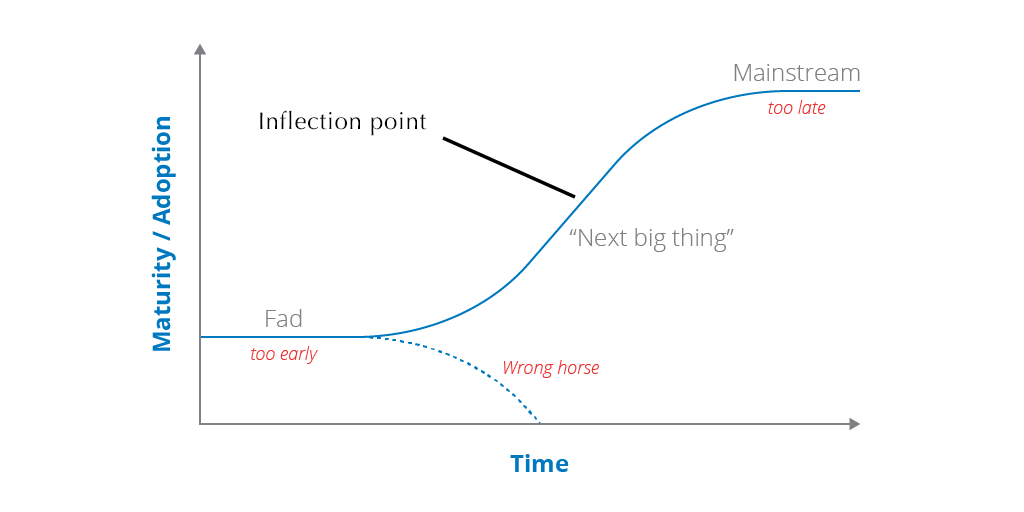
And if your strategy was to catch technologies there, I think you’d write a rather different article.
Absolutely. It’s even worse when they draw the inflection point on an exponential curve rather then a sigmoid.
Wow. Math snobbery at its best. There is clearly a difference between the strictly mathematical definition of this term and the more metaphorical, common use. But point taken: I will do my best not to “draw the inflection point on an exponential curve rather then a sigmoid.”
🙂
But yes, Spencer’s comment suggests a nice summary: you can’t have an inflection point unless part of your curve is S-shaped.